I
FRATTALI
I frattali sono particolari figure geometriche complesse, studiate da vari matematici negli ultimi due secoli (Julia, Cantor), ma portate a uno stadio avanzato di sviluppo da Benoit Mandelbrot negli anni Settanta. Con le avanzate tecnologie messegli a disposizione dalla IBM, Mandelbrot riuscì a far progredire di moltissimo gli studi su questa branca della matematica, forte di calcolatori con capacità molto superiori a quelli avuti a disposizione dagli altri matematici. Il frattale è una figura geometrica in cui un motivo identico si ripete su scala continuamente ridotta, teoricamente per infinite volte: ingrandendo la figura si otterranno sempre forme ricorrenti. Essi differiscono dagli oggetti geometrici tradizionali e dalle curve piane classiche perché non derivano da una funzione, cioè da un rapporto fra variabili esprimibile in un grafico, ma da un algoritmo, cioè un sistema di procedure di calcolo che portano alla soluzione di un problema in un numero finito di operazioni: questo genera un numero di forme e particolarità molto più alto. Inoltre, l’algoritmo che li genera è ricorsivo, cioè iterato infinitamente: questo genera l’autosimilarità del frattale, la proprietà per cui ogni parte più piccola è uguale alla figura intera e a ogni successivo ingrandimento si ripresenta sempre la stessa figura. La costruzione di un frattale parte da una figura di partenza cui si applica la trasformazione definita dall’algoritmo un numero infinito di volte, o meglio un numero di volte bastante per l’uso cui il frattale è destinato.
Ad esempio uno dei frattali più famosi, il Triangolo o Gerla di Sierpinski, deriva da un semplice quadrato. A tale quadrato si sottrae un quadrato più piccolo pari a un quarto della sua area in basso a sinistra, ottenendo una figura che può essere vista come l’unione di tre quadrati più piccoli. A ciascuno di essi viene applicato ancora il procedimento fino ad ottenere la figura finale.

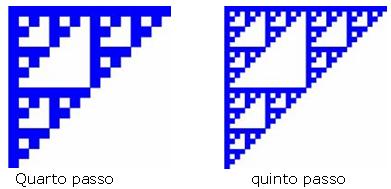
E così via…
In termini matematici, i punti del quadrato si sottopongono a tre traslazioni, così sintetizzabili, ponendo l’origine di un piano cartesiano nel vertice in basso a destra del quadrato:
1)X = ½x 2) X = ½x 3) X = ½x + ½
Y = ½y Y = ½y + ½ Y = ½y + ½

Dove x e y sono le coordinate iniziali dei punti rispetto all’origine, e X e Y sono le coordinate dei punti traslati. Nella figura a colori vediamo come la trasformazione 1) generi la parte in blu, la trasformazione 2) quella rossa, la trasformazione 3) quella verde:
Un frattale, come molte altre figure (retta, altre funzioni) non è interamente rappresentabile: siccome l’algoritmo deve essere ripetuto infinite volte, la forma definitiva che avrà il frattale è solo ipotizzabile, ma non ricreabile. Ciò genera il paradosso consistente nel sapere perfettamente come calcolare la forma del frattale ma nel non poterla in alcun modo realizzare. Tuttavia con lo sviluppo continuo della capacità di calcolo dei computer, si possono creare figure che hanno la stessa valenza matematica per la rappresentazione del frattale della valenza che ha segno su un foglio per la rappresentazione della retta. Esistono programmi in grado di compiere le operazioni per il disegno del frattale un numero di volte talmente alto da tracciare una figura assolutamente assimilabile al frattale vero e proprio sia per la semplice visualizzazione sia per le operazioni di calcolo (qualunque ulteriore ripetizione delle operazioni genererebbe differenze così infinitesimali da essere impercettibili).
1) Autosimilarità: F è unione di un numero di parti che, ingrandite di un certo fattore, riproducono tutto F; in altri termini F è unione di copie di se stesso a scale differenti.
2) Struttura fine: F rivela dettagli ad ogni ingrandimento.
3) Irregolarità: F non si può descrivere come luogo di punti che soddisfano semplici condizioni geometriche o analitiche: la funzione è ricorsiva, cioè infinitamente iterata.
4) Dimensione di autosimilarità > della dimensione topologica
La dimensione topologica di un insieme è il numero di parametri indipendenti necessari alla descrizione di un punto dell'insieme. Ad esempio, un punto sul piano è descritto da due parametri indipendenti (le coordinate cartesiane del punto) e, infatti, il piano è bidimensionale. Se l’insieme di riferimento fosse la retta il parametro presente sarebbe uno solo, la lunghezza, e infatti la retta è monodimensionale; lo spazio, infine, necessita di tre coordinate fondamentali (altezza, larghezza, profondità) ed ha dunque tre dimensioni. Ne consegue che la dimensione topologica dovrebbe essere sempre un numero naturale.
Il termine frattale
venne coniato nel 1975 da Mandelbrot, e deriva dal latino fractus,
in onore della loro dimensione frazionaria.
La natura produce molti esempi di forme molto simili ai frattali. Ad esempio in un albero (soprattutto nell'abete o nella felce) ogni ramo è approssimativamente simile all'intero albero e ogni rametto è a sua volta simile al proprio ramo, e così via; è anche possibile notare fenomeni di auto-similiarità nella forma di una costa: con immagini riprese da un satellite man mano sempre più ingrandite si nota che la struttura particolare di golfi e insenature mostra molte componenti che rassomigliano molto alla forma complessiva su scala più grande. Mandelbrot cominciò a studiare i frattali proprio approfondendo altri studi sulle irregolarità delle coste inglesi, scoprendo tantissime affinità fra tali figure e molte forme del mondo reale. Oggi si ritiene universalmente che i frattali possano descrivere il mondo in maniera molto più precisa e accurata che non le vecchie figure piane euclidee, che sono solamente approssimazioni delle forme reali. Gli utilizzi attuali della geometria frattale sono i più disparati: alcuni economisti hanno sviluppato teorie che arrivano a prevedere le oscillazioni del mercato secondo modelli matematici frattali, mentre c’è sempre maggior interesse sulla componente artistica della geometria frattale: si organizzano annualmente varie competizioni in merito, nelle quali artisti con sufficienti cognizioni matematiche possono presentare le loro creazioni. Ecco alcuni esempi:
"La morte nera"
"Zorro"
I frattali sono particolari figure geometriche complesse, studiate da vari matematici negli ultimi due secoli (Julia, Cantor), ma portate a uno stadio avanzato di sviluppo da Benoit Mandelbrot negli anni Settanta. Con le avanzate tecnologie messegli a disposizione dalla IBM, Mandelbrot riuscì a far progredire di moltissimo gli studi su questa branca della matematica, forte di calcolatori con capacità molto superiori a quelli avuti a disposizione dagli altri matematici. Il frattale è una figura geometrica in cui un motivo identico si ripete su scala continuamente ridotta, teoricamente per infinite volte: ingrandendo la figura si otterranno sempre forme ricorrenti. Essi differiscono dagli oggetti geometrici tradizionali e dalle curve piane classiche perché non derivano da una funzione, cioè da un rapporto fra variabili esprimibile in un grafico, ma da un algoritmo, cioè un sistema di procedure di calcolo che portano alla soluzione di un problema in un numero finito di operazioni: questo genera un numero di forme e particolarità molto più alto. Inoltre, l’algoritmo che li genera è ricorsivo, cioè iterato infinitamente: questo genera l’autosimilarità del frattale, la proprietà per cui ogni parte più piccola è uguale alla figura intera e a ogni successivo ingrandimento si ripresenta sempre la stessa figura. La costruzione di un frattale parte da una figura di partenza cui si applica la trasformazione definita dall’algoritmo un numero infinito di volte, o meglio un numero di volte bastante per l’uso cui il frattale è destinato.
Ad esempio uno dei frattali più famosi, il Triangolo o Gerla di Sierpinski, deriva da un semplice quadrato. A tale quadrato si sottrae un quadrato più piccolo pari a un quarto della sua area in basso a sinistra, ottenendo una figura che può essere vista come l’unione di tre quadrati più piccoli. A ciascuno di essi viene applicato ancora il procedimento fino ad ottenere la figura finale.


E così via…
In termini matematici, i punti del quadrato si sottopongono a tre traslazioni, così sintetizzabili, ponendo l’origine di un piano cartesiano nel vertice in basso a destra del quadrato:
1)X = ½x 2) X = ½x 3) X = ½x + ½
Y = ½y Y = ½y + ½ Y = ½y + ½

Dove x e y sono le coordinate iniziali dei punti rispetto all’origine, e X e Y sono le coordinate dei punti traslati. Nella figura a colori vediamo come la trasformazione 1) generi la parte in blu, la trasformazione 2) quella rossa, la trasformazione 3) quella verde:
Un frattale, come molte altre figure (retta, altre funzioni) non è interamente rappresentabile: siccome l’algoritmo deve essere ripetuto infinite volte, la forma definitiva che avrà il frattale è solo ipotizzabile, ma non ricreabile. Ciò genera il paradosso consistente nel sapere perfettamente come calcolare la forma del frattale ma nel non poterla in alcun modo realizzare. Tuttavia con lo sviluppo continuo della capacità di calcolo dei computer, si possono creare figure che hanno la stessa valenza matematica per la rappresentazione del frattale della valenza che ha segno su un foglio per la rappresentazione della retta. Esistono programmi in grado di compiere le operazioni per il disegno del frattale un numero di volte talmente alto da tracciare una figura assolutamente assimilabile al frattale vero e proprio sia per la semplice visualizzazione sia per le operazioni di calcolo (qualunque ulteriore ripetizione delle operazioni genererebbe differenze così infinitesimali da essere impercettibili).
DEFINIZIONE TECNICA
In realtà i frattali, essendo fra i principali oggetti di studio della matematica odierna e dunque una materia in continua evoluzione, non hanno ancora una definizione matematica precisa: l'atteggiamento corrente è quello di considerare frattale un insieme di punti F che abbia proprietà simili alle quattro elencate qui di seguito:1) Autosimilarità: F è unione di un numero di parti che, ingrandite di un certo fattore, riproducono tutto F; in altri termini F è unione di copie di se stesso a scale differenti.
2) Struttura fine: F rivela dettagli ad ogni ingrandimento.
3) Irregolarità: F non si può descrivere come luogo di punti che soddisfano semplici condizioni geometriche o analitiche: la funzione è ricorsiva, cioè infinitamente iterata.
4) Dimensione di autosimilarità > della dimensione topologica
La dimensione topologica di un insieme è il numero di parametri indipendenti necessari alla descrizione di un punto dell'insieme. Ad esempio, un punto sul piano è descritto da due parametri indipendenti (le coordinate cartesiane del punto) e, infatti, il piano è bidimensionale. Se l’insieme di riferimento fosse la retta il parametro presente sarebbe uno solo, la lunghezza, e infatti la retta è monodimensionale; lo spazio, infine, necessita di tre coordinate fondamentali (altezza, larghezza, profondità) ed ha dunque tre dimensioni. Ne consegue che la dimensione topologica dovrebbe essere sempre un numero naturale.
| Tuttavia i frattali, nonostante possano essere rappresentati in uno spazio convenzionale a due o tre dimensioni (pur con il metodo delle approssimazioni che abbiamo visto), hanno dimensione frazionaria. La lunghezza di un frattale "piano" non può essere misurata definitamene con l’ausilio delle semplici coordinate topologiche, ma dipende strettamente dal numero di iterazioni al quale si sottopone la figura iniziale: l’ordinaria definizione di dimensione è dunque venuta a perdere significato, e ne è stata universalmente adottata una molto più tecnica (la dimensione di Hausdorff) che ammette l’esistenza di dimensioni frazionarie. |
La natura produce molti esempi di forme molto simili ai frattali. Ad esempio in un albero (soprattutto nell'abete o nella felce) ogni ramo è approssimativamente simile all'intero albero e ogni rametto è a sua volta simile al proprio ramo, e così via; è anche possibile notare fenomeni di auto-similiarità nella forma di una costa: con immagini riprese da un satellite man mano sempre più ingrandite si nota che la struttura particolare di golfi e insenature mostra molte componenti che rassomigliano molto alla forma complessiva su scala più grande. Mandelbrot cominciò a studiare i frattali proprio approfondendo altri studi sulle irregolarità delle coste inglesi, scoprendo tantissime affinità fra tali figure e molte forme del mondo reale. Oggi si ritiene universalmente che i frattali possano descrivere il mondo in maniera molto più precisa e accurata che non le vecchie figure piane euclidee, che sono solamente approssimazioni delle forme reali. Gli utilizzi attuali della geometria frattale sono i più disparati: alcuni economisti hanno sviluppato teorie che arrivano a prevedere le oscillazioni del mercato secondo modelli matematici frattali, mentre c’è sempre maggior interesse sulla componente artistica della geometria frattale: si organizzano annualmente varie competizioni in merito, nelle quali artisti con sufficienti cognizioni matematiche possono presentare le loro creazioni. Ecco alcuni esempi:

"La morte nera"

"Zorro"